Què és un polígon de Thiessen?
El polígon del senador Saxian Tyson, també anomenat diagrama de Voronoi (diagrama de Voronoi), que rep el nom de Georgy Voronoi, és una forma especial de divisió de l'espai.

La seva lògica interna és un conjunt de polígons continus compostos per bisectrius verticals que connecten dos segments de línia de punts adjacents. La distància des de qualsevol punt d'un polígon de Thiessen fins al punt de control que constitueix el polígon és menor que la distància als punts de control d'altres polígons, i cada polígon conté una i només una mostra.
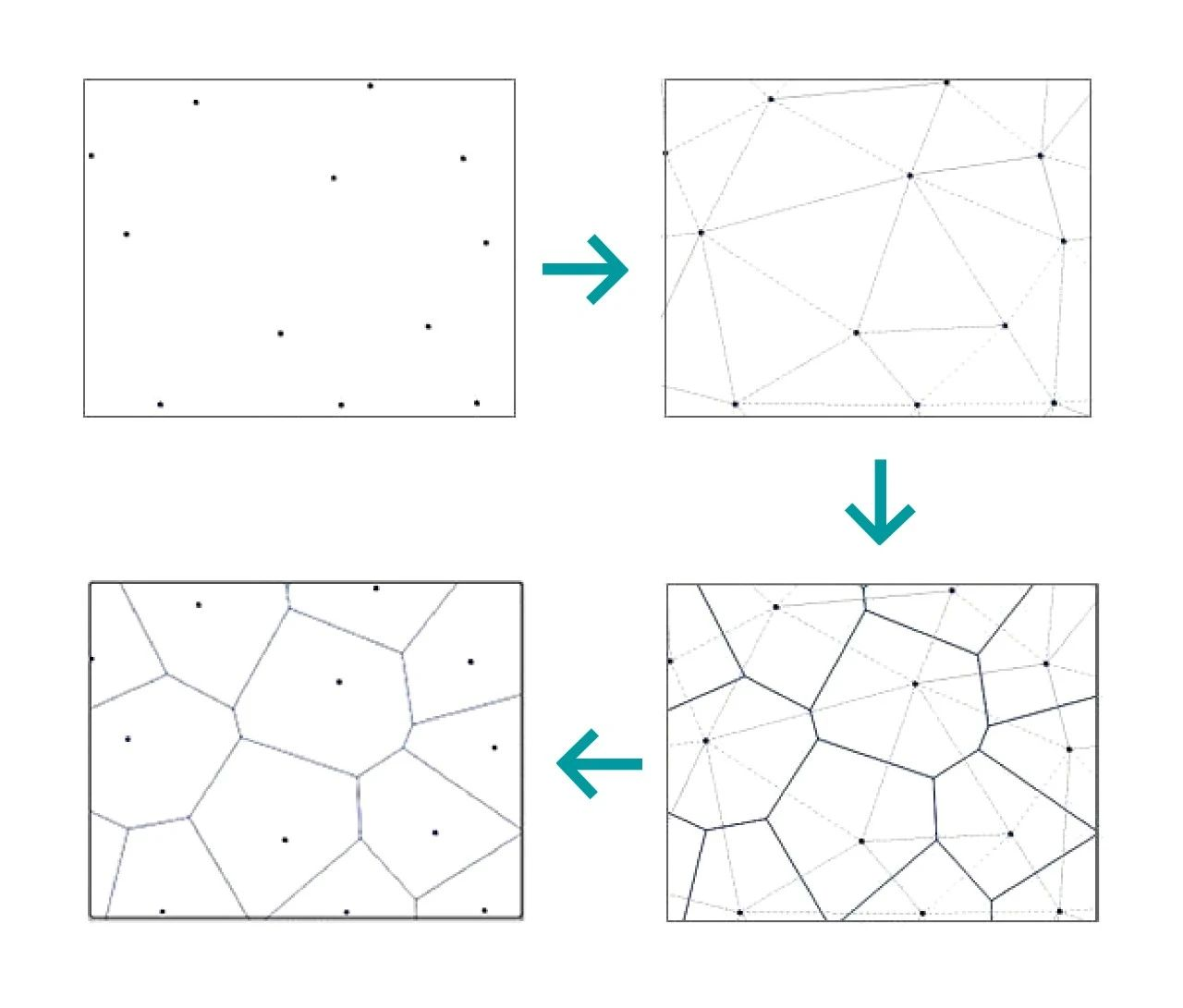
L'aspecte únic i meravellós dels polígons Tyson té aplicacions en arquitectura, etc. L'aspecte del cub d'aigua i el disseny paisatgístic dels parcs s'apliquen als polígons Tyson.


El principi de la barreja de llum del polígon de Tyson:
Actualment, les lents del mercat sovint utilitzen superfícies quadrilàteres, hexagonals i altres tipus de perles per a la barreja de llum, i totes aquestes estructures tenen formes regulars.
La llum emesa per la font de llum es subdivideix per cada petita superfície de perla a través de la lent i, finalment, se superposa a la superfície receptora per formar un punt de llum. Les superfícies de perles de diferents formes poden assignar diferents punts de llum, de manera que s'utilitzen superfícies de perles amb formes regulars com ara quadrilàters i hexàgons. El punt de llum format també es forma per la superposició d'una pluralitat de punts de llum quadrangulars i hexagonals.
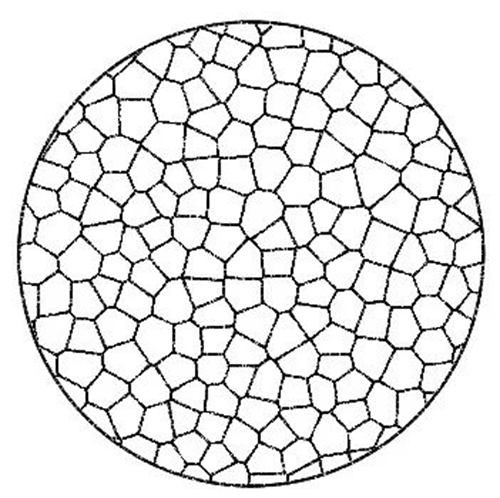
La superfície de la perla del polígon de Thiessen utilitza la forma inconsistent de cada polígon de Thiessen per superposar-se i formar un punt de llum. Quan la superfície de la perla té un nombre suficient, es pot superposar per formar un punt de llum circular uniforme.
Contrast puntual
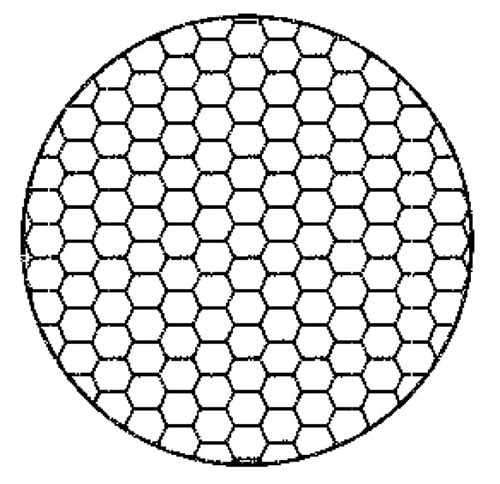
La figura següent mostra el punt de llum format per la superposició de tres superfícies de perles: quadrilàter, hexàgon i polígon de Thiessen, i el nombre de superfícies de perles i el radi R dels tres tipus de superfícies de perles són els mateixos sota la mateixa àrea emissora de llum.

cara de perla quadrilàtera

Cara de perla hexagonal

Cara de perles poligonals Tyson
De la comparació dels tres punts de llum de la imatge superior, és obvi que el punt de llum format per la superposició dels polígons de Tyson a la imatge de la dreta s'assembla més a un cercle, i el punt de llum serà més uniforme. Es pot veure que la capacitat de barreja de llum de la superfície de la perla del polígon de Tyson és més forta.
Lent poligonal Shinland Tyson
Data de publicació: 10 de juny de 2022








