Что такое многоугольник Тиссена?
Многоугольник Саксиан Сен. Тайсона также называется диаграммой Вороного (диаграмма Вороного), названной в честь Георгия Вороного, представляет собой особую форму разбиения пространства.
Его внутренняя логика представляет собой набор непрерывных многоугольников, состоящих из вертикальных биссектрис, соединяющих два смежных отрезка. Расстояние от любой точки многоугольника Тиссена до контрольной точки, составляющей этот многоугольник, меньше расстояния до контрольных точек других многоугольников, и каждый многоугольник содержит один и только один образец.
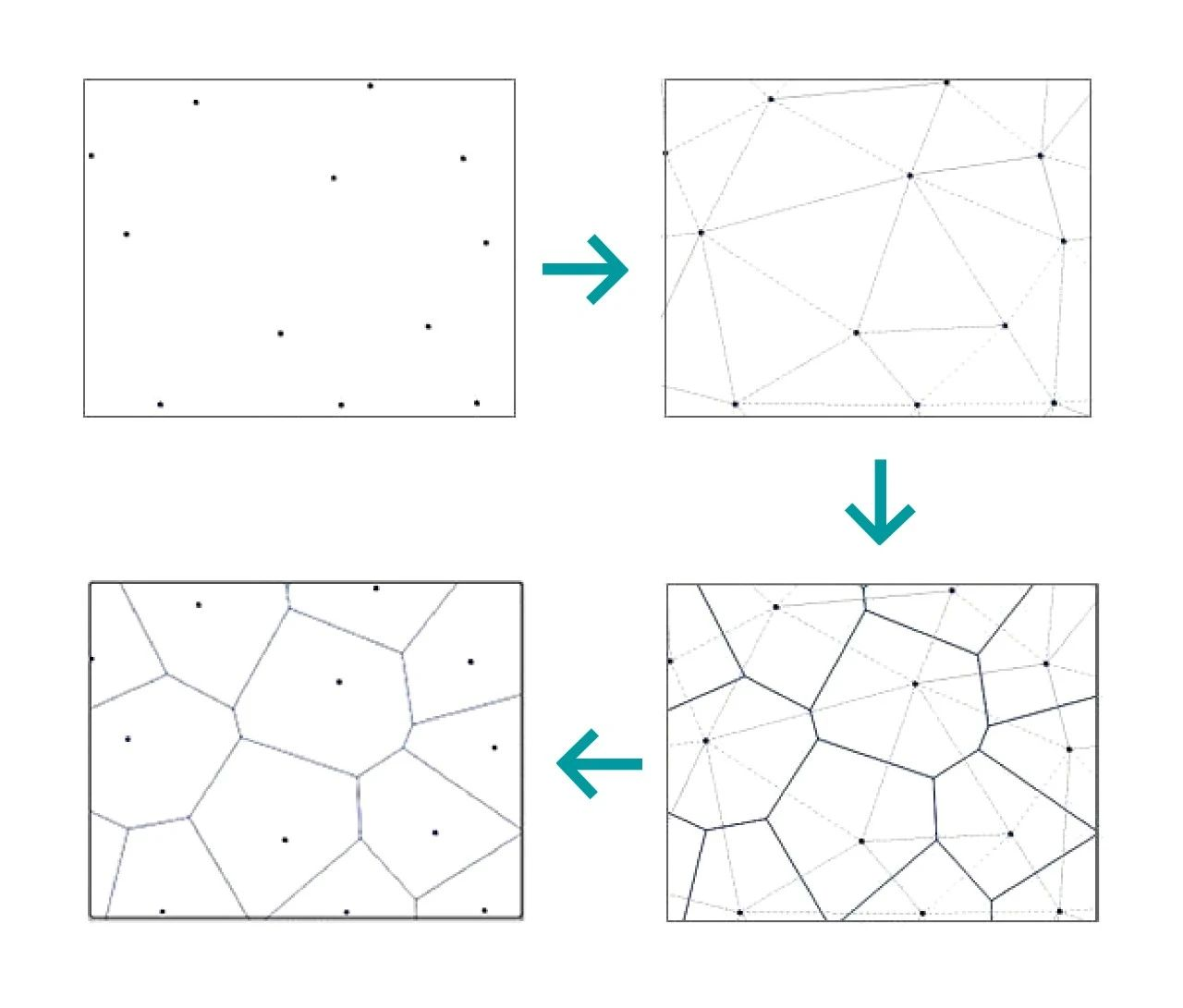
Уникальный и замечательный внешний вид полигонов Тайсона нашел применение в архитектуре и т. д. Внешний вид водного куба и ландшафтный дизайн парков нашли свое применение в полигонах Тайсона.
Принцип смешивания света полигона Тайсона:
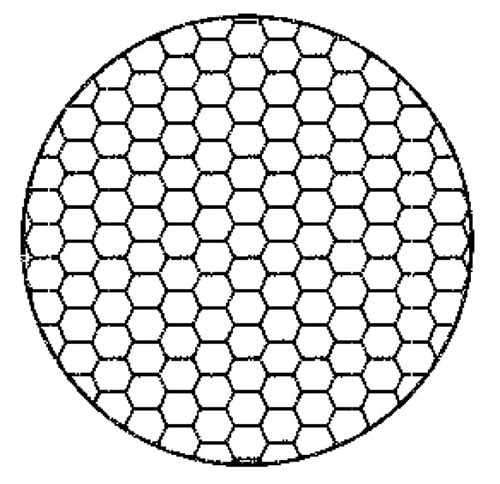
В настоящее время на рынке линзы часто используют четырехугольные, шестиугольные и другие поверхности с шариками для смешения света, и все эти структуры имеют правильную форму.
Свет, излучаемый источником света, разделяется каждой мелкой поверхностью шарика через линзу и, наконец, накладывается на принимающую поверхность, формируя световое пятно. Поверхности шариков разной формы могут формировать различные световые пятна, поэтому используются поверхности шариков правильной формы, такие как четырёхугольники и шестиугольники. Формируемое световое пятно также формируется путём наложения множества четырёхугольных и шестиугольных световых пятен.
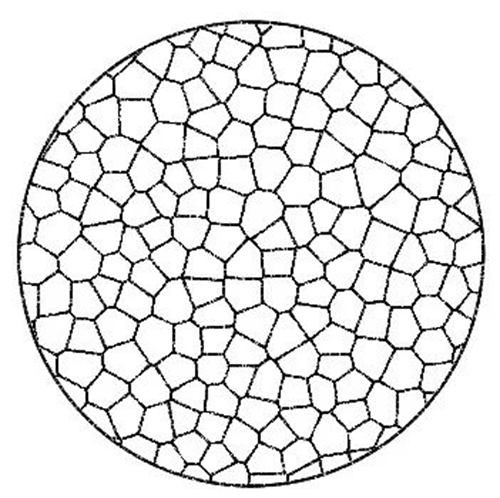
Поверхность полигональных бусин Тиссена использует неоднородную форму каждого полигона Тиссена для наложения друг на друга, формируя световое пятно. При наличии достаточного количества бусин на поверхности их можно наложить друг на друга, чтобы сформировать равномерное круглое световое пятно.
Точечный контраст
На рисунке ниже показано световое пятно, образованное суперпозицией трех поверхностей шариков: четырехугольника, шестиугольника и многоугольника Тиссена, причем количество поверхностей шариков и радиус R трех типов поверхностей шариков одинаковы при одной и той же площади светоизлучающей способности.
четырехугольная грань бусины
Шестиугольная грань бусины
Тайсон Полигон Бид Фейс
Сравнивая три световых пятна на изображении выше, очевидно, что световое пятно, образованное суперпозицией полигонов Тайсона на правом изображении, ближе к кругу и более равномерно. Видно, что светосмешение поверхности полигонов Тайсона сильнее.
Линза Shinland Tyson Polygon
Время публикации: 10 июня 2022 г.
